用懸滴法（Pendant Drop method）來測量液體的表面和界面張力已有很長的歷史。早在 19世紀末（1882），Bashforth和Adams就在Young-Laplace公式的 基礎上，推導出了描述一個處于靜力（界面張力對重力）平衡時的懸滴輪廓的方程式（Eq. of Bashforth and Adams）[1]：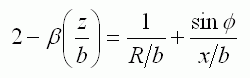
1) 懸滴法示意圖
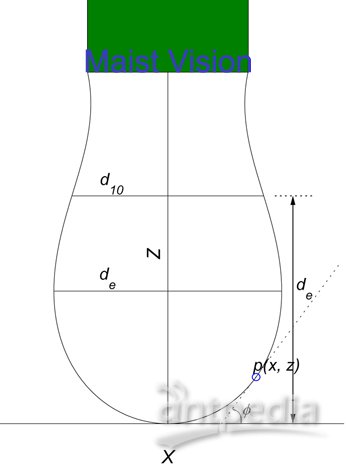上式中（參見圖1），b為懸滴底端（apex）的曲率半徑，R為懸滴輪廓上一點p(x, z)在紙平面上的主曲率半徑（principle radius of curvature），φ為輪廓線上p(x, z)點處的切線與x軸的夾角。β是體系的Bond number，在這里往往被稱為液滴的形狀因子（shape parameter），因為它的值直接決定了液滴的形狀（注意：是指形狀，不涉及其大小）：
Δρ為液滴相與周圍相之間的密度差； g為重力加速度；γ為表面/界面張力； α為體系的毛細管常數（capillary constant）。
從上面的方程式可以看出：一個懸滴在達到靜力（界面張力對重力）平衡時，其輪廓可通過懸滴底端 （apex）的曲率半徑b和液滴的形狀因子β來確定。反之也然： 若能夠確定b和β，也就確定了懸滴的輪廓。
Bashforth and Adams通過對（1）式的計算制定出了相應的懸滴輪廓數據表，并通過對真實懸滴輪廓的直接測量進行了檢驗。運用這一表格，原則上就可通過測量一懸滴的輪廓來獲得液體的表面張力。但基于當時條件的限制，實踐使用起來相當不方便。為了簡化這一步驟，Andreas等[2]在1938年（通過對由水形成的各種形狀的懸滴的直接測量）引入了經驗較正因子，使得可通過測量懸滴輪廓兩極限位置處的尺寸來計算出液體的表面張力，也即所謂的Selected-Plane Method（選擇平面法或選面法）。Stauffer和Fordham [3，4] 后來通過對 Bashforth-Adams方程的求解準確地獲得了這一較正因子，并列成表格。 后來Roe [5] 進一步引入多選擇平面法，也即通過測量懸滴輪廓多處極限位置的特征尺寸來提高計算的可靠性和準確性。從那時起懸滴法就成為一經典的表/界面張力測量法。測量通常是通過對液滴拍照，然后通過對照片上液滴幾處選擇平面上尺寸的測量，再通過查表，就可獲得表/界面張力的值（當界面兩相的密度差已知時）。
雖然當時人們就知道懸滴法是一很可靠、準確的方法，但受當時條件的限制，使得實踐操作很煩人，數據又要等到照片沖洗出來后才可獲得，使得這一方法的使用不廣，多數只是局限于實驗室里研究使用。
1980年代到1990年代，隨著計算機技術和數字圖像技術的發展，懸滴法又得到了應有的重視，并逐步被完全計算機數字化。這不但使其成為最易于操作的測量方法，而且其測量的準確性和可靠性也獲得了進一步的提高。1990年代末，首批商品化的懸滴法測量儀進入市場，從而開始了懸滴法的普遍應用階段。
但即使引入了計算機和數字圖像處理，現在市場上供應的懸滴法仍可分為二類：
基于數字圖像的選擇平面法（selected-plane(s) method）
基于數字圖像的完整液滴輪廓法（whole drop profile analysis）
第一種方法只是通過對獲得的數字圖像進行如圖1所示的 de和d10的測量，再通過查表獲得校正因子，從而得到液體的表面張力。它是“現代“的傳統方法，其精度不會比從前的傳統方法高，因為數字圖像的坐標分辨率是有限的，而最終的表面張力值對de和d10測量中的任何微小誤差都很敏感。而且這種方法的局限性大，因為只有呈現出 de (最大直徑)的懸滴才可以被測量，而且當懸滴的長/寬比不是很大時，d10/de的比值對表面張力的值的變化不是很敏感。這種方法的精度一般很難超過2～3%，當懸滴的長/寬比接近1時（也即懸滴接近球形時）其誤差更可高達20% [3]。市場上供應的有些懸滴法甚至只依靠用戶的鼠標點擊操作來測量 de和d10，這樣做的精度一般不會超過5%，且測量結果很受主觀因素以及操作者經驗的影響。
2a) 懸滴圖像
2b) 懸滴圖像的輪廓坐標（紅線）
2c) 懸滴圖像輪廓坐標的理論擬合線（綠線）
3) 水/甲苯-體系界面張力的測量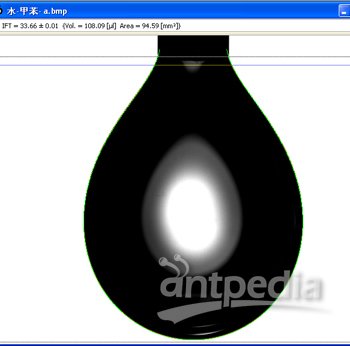
現代的完全數字、計算機化的懸滴法是由一攝像機/相機抓取一懸滴的圖像，并將整個圖像數字化。數字化后的圖像由計算機進行圖像處理，測定其整個懸滴輪廓的坐標（可多致幾千個坐標點），而且坐標測量的可達到亞像素（sub-pixel）精度。通過將后者擬合到描述懸滴輪廓的Bashforth-Adams方程式（1），就可得到毛細管常數a。在知道了界面兩相的密度差和重力加速度的情況下，就可由 a 計算出界面的表/界面張力值（見圖2）。在擬合過程中，計算方法不但考慮了表面的毛細管常數以及液滴的本身參數，而且將幾乎所有的可能影響因素如圖像成像過程中的可能形變，懸滴圖像相對于相機的相對旋轉角度（由于相機的放置不可能100%水平），圖像的可能對焦（focus）偏差等都考慮在內。整個過程根本不需要用戶任何介入，而且整個計算過程在短于一秒內就能完成，真正做到快速、準確和不受主觀因素影響。這種方法的精度在一般實驗條件下就可以達到約0.1%。我們的軟件使用的就是這樣的方法。
盡管懸滴法在學術界已是一公認的通用性廣、可靠性高而且操作又間便的方法，與其他的經典測量方法相比，懸滴法的著名度急待提高，真正了解、使用過它的人還不多。多數人了解、接觸到的表面張力測量方法仍然是經典的測量方法如Du Nouy吊環法和Wilhel-my Plate薄板法，而對懸滴法只是聽說而已。其實與這些經典的測量方法相比，懸滴法有其很明顯的特點和優點：
懸滴法是一種絕對的測量方法（absolute method）。說它絕對是因為它不像其它的方法需要作種種的假設，如Du Nouy吊環法和Wilhelmy Plate法都要假設 被測的液體能完全潤濕吊環或薄板，吊環或薄板在接觸界面時必須與液面保持平行，而且所用的吊環或薄板的真正幾何尺寸事實上往往需要通過測量已知表面張力的液體（而且往往選用水）來校正。
懸滴法的僅有假設有二：1）液滴處于表面張力和重力的靜力平衡；2）懸滴呈中心軸（圖1中的Z-軸）對稱。對于粘度在100 Pa·s 以下的液體，其實要做到這二點并不難（如對第2）點，只要保證形成的懸滴不要太小就基本可達到）。基于數字圖像的懸滴法唯一需要校正的，或者更準確地說，需要測量的是圖像的放大倍數，這可通過對已知尺寸的、用來形成懸滴的毛線管/針管的圖像的同時測量來獲得，由此引入的系統誤差可控制在0.1%左右。
操作最簡便、省時。懸滴法在計算機數字化后已成為所有方法中操作上最方便、簡易的方法，能很快取得準確可靠的結果。測量一液體的表面張力應可在數分鐘內完成。
測量范圍廣：小至約0.001mN/m，大到上百上千mN/m都可用這一方法測量。沒有其它的經典測量方法可與此相比擬。
測量精度高，重復性好：如前所述，現代的、基于液滴整個輪廓分析的懸滴法在一般實驗條件下精度就可以達到約0.1%。這一精度可與最準確的經典測量方法相比美。
是所有方法中液體用量最小的方法。液滴小至約10微升就能準確測定，所以原則上只需要幾十微升的液體就可測量。
測量的探針對形成的表/界面施加的影響最小：液滴事實上只與管端口的截面或管的外管壁（如果液體能很好潤濕管壁的話）有少量接觸，此一接觸面積與整個液滴的表面積相比是很小的。這對研究表面活性劑體系以及其它的自組織體系尤其重要，因為經典的測量方法如Du Nouy吊環法和Wilhelmy Plate 薄板法很難避免使 用的吊環或薄板本身對表面活性劑（或其它的自組織體系）在表面的吸附（absorption）和分子的組織排列產生影響。
對液體的粘度最不敏感：由于上述的很小的接觸面積，使得液滴能很快達到平衡，所以懸滴法是最適合測量高粘度液體的方法。事實上如果一液體由于粘度太大而無法用懸滴法測量，也就很難找到其他的合適方法。正是由于這一原因，懸滴法被廣泛用來測量高粘度的高分子融體和高分子溶液的表/界面張力。
非常適合高溫、高壓下的測量。懸滴法常被用于溫度高達上千度，壓力高達幾百巴的環境下的測量。
適用于進行動態測量：可從表/界面形成后的約0.1秒（甚至可低到幾十微妙）起，對表/界面進行時間依賴性測量（可長至幾小時，幾天，...）。此方法的動態測量尤其適合研究表面活性劑體系。不但可以考察表面活性劑的擴散速度，而且可以測量CMC，表面活性分子在表面所占的面積等。
適用于進行表面粘/彈性（Surface Rheology）的研究：在適當硬件的支持下（ 如高精度注射泵或壓電單元），懸滴的表面積或體積都可以得到控制，并使其隨著時間按某一模式發生變化，同時跟蹤液滴界面表面張力的變化，就可分析得到體系（界面）的粘/彈性模量，這對研究乳化劑的性能很有幫助。懸滴的表面積其實是一微形的Langmuir槽 （Trog），許多以前得運用Langmuir槽的研究工作，不少可以通過懸滴法來代替，同時大大減少了液體的用量。
基于懸滴法的以上優點和特點，其重要性必將愈來愈受到人們的認識和重視。我們有充足的理由相信，在不久的將來，懸滴法將成為最重要并被廣泛使用的表/界面測量方法之一，而且其應用的領域也將隨著研究的深入和技術的完善得以不斷地擴大。
注：與懸滴法相對應的另一方法是上升氣泡（rising bubble）法。
參考文獻：
S. Bashforth and J. C. Adams, An Attempt to Test the Theory of Capillary Action, Cambridge University Press and Deighton, Bell & Co., London, 1892.
J. M. Andreas, E. A. Hauser, and W. B. Tucke, J. Phys. Chem., 42, 1001(1938)。
S. Fordham." On the Calculation of Surface Tension from Measurements of Pendant Drops." Proc. R. Soc. London. Ser. A. A194. 1 (1948).
C. E. Stauffer, "The Measurement of Surface Tension by the Pendant Drop Technique." J. Phvs. Chem., 69,1933 (1965).
R. J. Roe, V. L. Bacchetta and P. M. G. Wong, J. Phvs. Chem., 71,4190 (1967).
N. K. Adam. The Physics and Chemistry of Surfaces. 3rd ed.; p. 365. Oxford University Press. 1941.
J.F . Paddav, " The Measurement of Surface Tension"; pp. 110-12 in Surface and Colloid Science. Vol. 1. Edited by E. Matijevic. Wiley Interscience. New York,1969.
J. F. Padday. "The Profile of Axially Symmetric Menisci," Philos. Trans. R. Soc. London. Ser. A. A269. 265 (1971).
J. F. Paddav and A. Pitt, "Axisymmetric Meniscus Profiles," J . Colloid Interface Sci., 38 [2] 1972.
P. G. de Gennes, F. Brochard-Wyart; D. Quéré, Capillary and Wetting Phenomena — Drops, Bubbles, Pearls, Waves. Springer 2002.
Adamson, A.W. Physical Chemistry of Surfaces, 2nd Edition, Wiley, interscience, New York, pp 9-41, 1967.
Anastasiadis, S.H.; Chen, J.K.; Kobertein, J.T.; Siegel, A F.; Sohn, J.E.; Emerson, J.A. J. Colloid Interface Sci, v. 119, p. 55, 1986.