前言
相信每一位使用過HFSS的工程師都有一個疑問或者曾經有一個疑問:我怎么才能使用HFSS計算的又快又準?對使用者而言,每個工程師遇到的工程問題不一樣,工程經驗不能夠直接復制;對軟件而言,隨著HFSS版本的更新,HFSS算法越來越多,針對不同的應用場景對應不同的算法。因此,只有實際工程問題切合合適的算法,才能做到速度和精度的平衡。工程師在了解軟件算法的基礎上,便能夠針對自己的需求進行很好的算法選擇。
由于當今世界計算機的飛速發展,讓計算電磁學這門學科也有了很大的發展,如圖1所示,從大的方面來看,我們將計算電磁學分為精確的全波算法和高頻近似算法,在每一類下面又分了很多種算法,結合到HFSS軟件,通過ANSYS公司40余年來堅持不懈的研發和戰略性的收購,到目前為止,HFSS有FEM、IE(MoM)、DGTD、PO、SBR+等算法,本文會針對每種算法和應用場景逐一介紹,相信你看完這篇文章應該對HFSS算法和應用場景會有更深的認識。
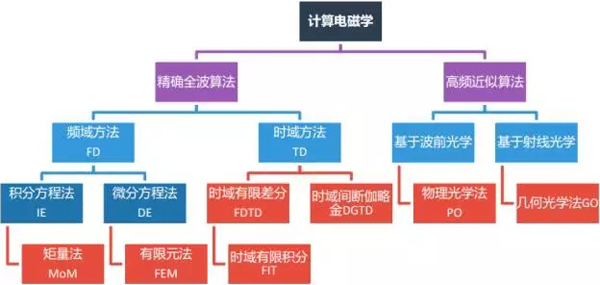
圖1、計算電磁學
算法介紹
全波算法-有限元算法(FEM)
有限元算法是ANSYS HFSS的核心算法,已有二十多年的商用歷史,也是目前業界最成熟穩定的三維電磁場求解器,有限元算法的優點是具有極好的結構適應性和材料適應性,充分考慮材料特性:趨膚效應、介質損耗、頻變材料;是精確求解復雜材料復雜結構問題的最佳利器,有限元算法采用四面體網格,對仿真物體能夠很好的進行還原。
FEM算法的支配方程見下圖:
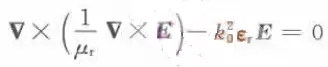
圖2、FEM算法支配方程
HFSS有限元算法在網格劃分方面能夠支持自適應網格剖分、網格加密、曲線型網格,在求解時支持切向矢量基函數、混合階基函數和直接法、迭代法、區域分解法的強大的矩陣求解技術。
在應用領域,HFSS主要針對復雜結構進行求解,尤其是對于一些內部問題的求解,比高速信號完整性分析,陣列天線設計,腔體問題及電磁兼容等應用場景,非常適合有限元算法求解。
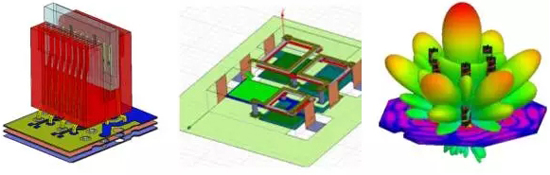
圖3、FEM算法應用場景
有限元算法結合ANSYS公司的HPC模塊,ANSYS HFSS有限元算法可以進行電大尺寸物體的計算,大幅度提升仿真工程師的工作效率。針對寬帶問題,FEM推出了寬帶自適應網格剖分,大大提升了仿真精度。
全波算法-積分方程算法(IE)
積分方程算法基于麥克斯維方程的積分形式,同時也基于格林函數,所以可自動滿足輻射邊界條件,對于簡單模型及材料的輻射問題,具有很大的優勢,但原始的積分方程法計算量太大,很難用于實際的數值計算中,針對此問題,HFSS 中的IE算法提供了兩種加速算法,一種是ACA 加速,一種是MLFMM,分布針對不同的應用類型。ACA 方法基于數值層面的加速技術,具有更好的普適性,但效率相比MLFMM 稍差,MLFMM 算法基于網格層面的加速,對金屬材料,松散結構,具有更高的效率。
IE算法的支配方程見下圖:
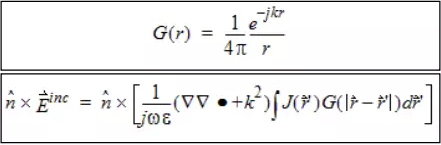
圖4、IE算法支配方程