混合算法(FEBI,IE-Region,PO-Region,SBR+ Region)
前面對頻率內的各種算法做了介紹并說明了各種算法應用的場景,很多時候碰到的工程問題既包括復雜結構物理也包括超大尺寸物理,如新能源汽車上的天線布局問題,對仿真而言,最好的精度是用全波算法求解,最快的速度是采用近似算求解,針對該問題,ANSYS公司將FEM算法、IE 算法、PO 算法、SBR+算法等融合起來,推出混合算法。在一個應用案例中,采用不同算法的優點而回避不同算法的缺點,可極大限度的提高算法的效率,以及成為頻域內解決大型復雜問題的必備算法。
HFSS中FEM與IE可以通過IE Region與FEBI邊界進行混合求解,FEM與PO、SBR+算法可以通過添加PO Region及SBR+ Region進行混合,混合算法的使用擴大了HFSS的使用范圍。
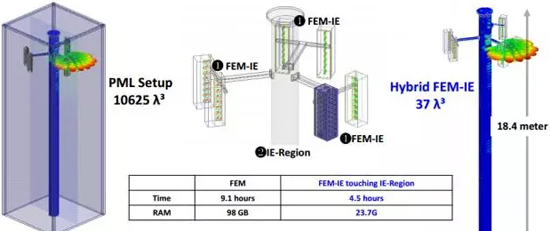
圖9、FEM與IE混合求解與FEM對比
時域算法-transient算法
HFSS時域求解是基于間斷伽略金法(discontinuous Galerkin method, DGTD)的三維全波電磁場仿真求解器,采用基于四面體有限元技術,能得到和HFSS頻域求解器一樣的自適應網格剖分精度,該技術使得HFSS的求精精度成為電磁場行業標準。這項技術完善了HFSS的頻域求解器技術,幫助工程師對更加深入詳細了解其所設計器件的電磁性能。
Transient算法支配方程見下圖:
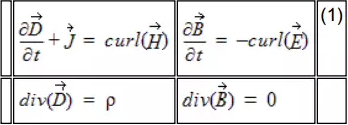
圖10、Transient算法支配方程
采用HFSS-Transient算法,工程師可利用短脈沖激勵對探地雷達、靜電放電、電磁干擾、雷擊和等應用問題開展研究,還包括時域反射阻抗以及短時激勵下的瞬態場顯示也可以借助它來完成。
圖11、Transient算法應用場景
諧振分析-Eigenmode算法
諧振特性是每個結構都存在固有的電磁諧振,諧振的模式、頻率和品質因子,與其結構尺寸相關,這些諧振既可能是干擾源的放大器,也可能是敏感電路的噪聲接收器。諧振會導致信號完整性、電源完整性和電磁兼容問題,因而了解諧振對加強設計可靠性很有幫助。
Eigenmode算法支配方程見下圖:

圖12、Eigenmode算法支配方程