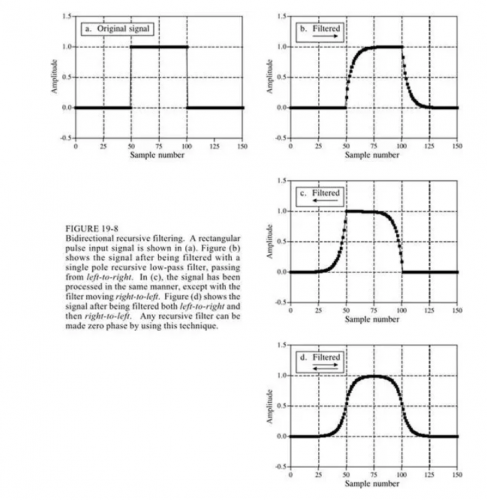
為了使IIR實現線性相位,可以進行雙向運算,如下圖所示:
切比雪夫濾波
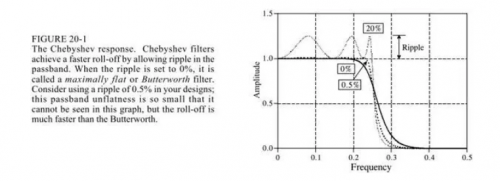
切比雪夫(Chebyshev)濾波是應用在頻域上分頻的,性能上當然不能和sinc窗函數濾波相比,但是它速度很快。
切比雪夫響應是一種數學策略,通過允許頻率響應中的紋波來實現更快的滾降。隨著波紋增加(壞),滾降變得更尖銳(好)。
對于極點的理解:
極點越多,性能越好。
通過查表可以確定濾波器的系數。
各種濾波器比較
1.模擬vs數字
如果信號需要濾波,是在模擬階段濾波呢?還是數字化之后濾波?
下圖做了比較,可以看到數字濾波有著模擬濾波難以達到的性能,但是速度慢,而且模擬濾波的幅度以及頻率的動態范圍更大。
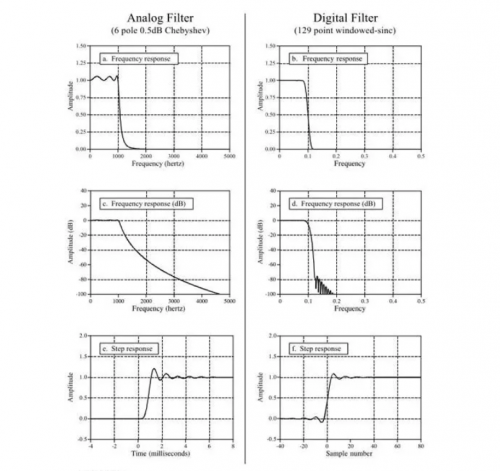

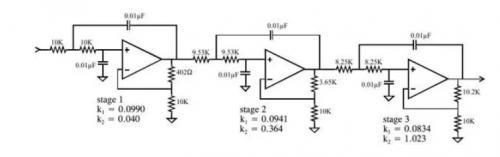
本例中模擬濾波的實現:
2.sinc窗函數vs切比雪夫
下圖做了比較
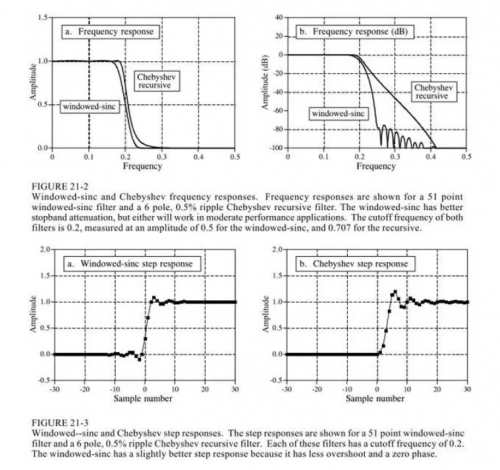
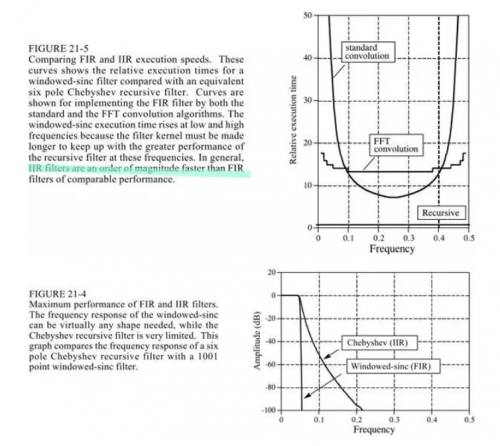
sinc窗函數是用卷積來運算,而切比雪夫是用遞歸方程。當然卷積可以用fft卷積來做,即先DFT然后頻域四則運算再DFT逆變換,這能提高速度,但是還是沒有遞歸方程快。另一方面sinc窗函數的濾波性能可以做的很好。
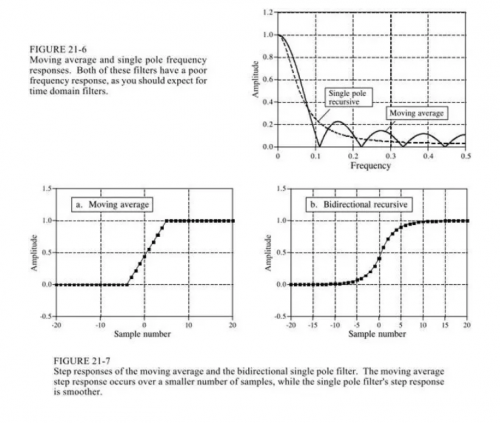
3.滑動平均vs單極點